マルコフ過程とは?状態遷移を利用した確率的未来予測手法
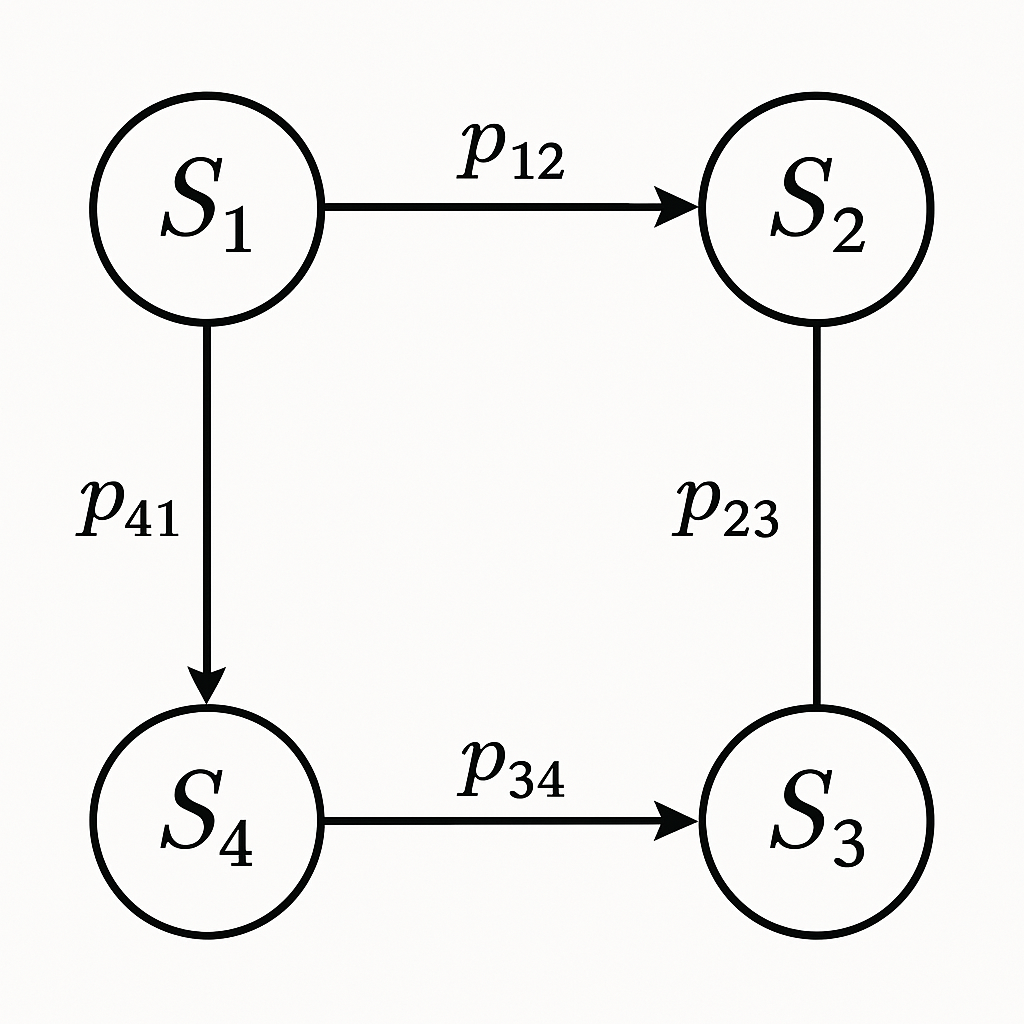
マルコフ過程は、未来の状態が現在の状態のみに依存する確率過程です。
現在の状態をもとにして次の状態が決定されるため、過去の情報は直接影響しません。
情報技術や統計学など多方面で利用され、システム解析やシミュレーションに役立ちます。
シンプルな考え方ながら、遷移行列を用いた詳細な解析も可能で、複雑な現象のモデリングに貢献しています。
マルコフ過程の基本
定義とマルコフ性
現在の状態に依存する仕組み
マルコフ過程は、今の状態だけに注目して未来を予測する方式です。
この仕組みでは、現在の状態から次の状態へ移行する可能性が、直前の状態にのみ基づいて決まります。
- 過去の情報は反映されず
- 現在の状態がすべての鍵となります
過去状態との無関係性
過去にどのような状態があったかは、未来の状態には影響しません。
この特徴のおかげで、計算がシンプルになり、複雑な履歴の管理が不要となります。
数学的表現
状態遷移の数式 P(Xₙ₊₁=j | Xₙ=i)=p₍ᵢⱼ₎
この数式は、現在の状態 i から次の状態 j に移る確率を示しています。
P(Xₙ₊₁=j | Xₙ=i)は状態jに移る条件付き確率p₍ᵢⱼ₎が各状態間の移行の強さを表しています
遷移行列の解説
状態間の全移行確率をひとまとめにしたものが遷移行列です。
遷移行列は、各行が現在の状態、各列が次の状態に対応し、以下のような構造となります。
- 各要素
p₍ᵢⱼ₎は状態iからjへの移行確率 - 行の合計は
1となる
例として、3つの状態 A, B, C が存在する場合、遷移行列は以下のような表になる場合があります。
| A | B | C | |
|---|---|---|---|
| A | 0.3 | 0.5 | 0.2 |
| B | 0.1 | 0.7 | 0.2 |
| C | 0.4 | 0.4 | 0.2 |
実例による理解
天気予測の例
天気の変化は、マルコフ過程の概念を理解するのに適しています。
- 「雨」「晴れ」「曇り」などの状態が存在し、1日の天気から翌日の天気に移行する例を考える
- 前日の天気が「雨」の場合、翌日が「晴れ」になる確率は前日のみの情報に依存する
この例では、過去の2日目以降の天気は考慮せず、1日に注目することでシンプルに予測が可能となります。
状態遷移の解析方法
遷移行列の解析
各要素の意味と役割
遷移行列の各数字は、状態間の移行可能性を表しています。
- 数値が大きいほど、移行の可能性が高くなります
- 数字の配置により、状態の関係性を視覚的に把握できます
定常状態の計算
定常状態とは、時間が十分に経過した後に各状態に到達する確率の安定した分布のことです。
- 遷移行列の累乗計算によって、各状態の確率の変化を追跡する
- 定常状態は、長期的なシステムの挙動の理解に役立ちます
数値シミュレーション
シミュレーション手法の概要
数値シミュレーションを用いると、実際の状態遷移を模倣することができます。
- 多くの場合、乱数を使って状態間の移行を再現する
- シミュレーションにより理論以外の実践的な結果を得ることが可能となる
解析結果の評価
シミュレーションの結果は、以下のポイントで評価されます。
- 遷移行列の理論との一致具合
- 定常状態への収束の速さ
- 予測値と実際の観測結果との比較
数値シミュレーションは、実践的な応用の前にシステムの挙動をチェックする手段として広く利用されます。
情報技術への応用事例
システムモデリングへの活用
アルゴリズムへの影響
アルゴリズム開発において、マルコフ過程の考え方は多くのシステムに貢献しています。
- 状態の変化をシンプルにモデル化できる
- 複雑なシステムでも予測モデルが作りやすくなります
パターン認識との関連
画像認識や音声認識など、パターン認識分野でマルコフ過程が利用されることがあります。
- シーケンスデータの変遷を扱う際に効果的
- ノイズの多いデータから有用なパターンを抽出する補助的ツールとして機能します
データ解析での利用例
予測モデルとの統合
ビッグデータ解析では、マルコフ過程を活用した予測モデルが数多く提案されています。
- 遷移行列を用いることで、データの時間変化を捉える
- 未来の状態の確率分布を算出し、リスク管理などに役立てる
シミュレーションの実装例
実装に際しては、プログラミング言語を用いたシミュレーションが行いやすい。
- PythonやRなどでライブラリが豊富に提供されている
- 以下のような簡単なコード例も参考になる
import numpy as np
# 状態数
states = ['A', 'B', 'C']
# 遷移行列設定
transition_matrix = np.array([
[0.3, 0.5, 0.2],
[0.1, 0.7, 0.2],
[0.4, 0.4, 0.2]
])
# 初期状態
current_state = 0
# シミュレーション実施
steps = 10
for i in range(steps):
current_state = np.random.choice(len(states), p=transition_matrix[current_state])
print(f"Step {i+1}: {states[current_state]}")関連分野との連携
統計学との融合
時系列解析との違い
時系列解析も未来予測に力を発揮するが、マルコフ過程は直近の状態のみを考慮する点に独自性があります。
- 時系列解析は長期的な依存関係を扱うことが多い
- マルコフ過程はシンプルなモデルで高速な計算が可能になる
実用性の検証
統計学の手法と組み合わせることで、マルコフ過程の予測精度をさらに向上させる工夫が見られます。
- 実データを用いて精度検証を実施
- 異なるモデルとの比較を通じ、最適な手法を選定するケースが多い
産業応用の展望
現状の課題と今後の可能性
現状、マルコフ過程は多くの分野で実用化されているが、いくつかの課題も存在します。
- 状態の選び方や遷移確率の推定が難しいケースがある
- さらなるアルゴリズムの洗練により、応用範囲は一層広がると期待される
実際の事例分析
実際の産業現場では、以下のような事例が確認されています。
- 在庫管理システムにおける需要予測
- ユーザー行動のモデリングによるマーケティング最適化
- ネットワーク異常検知におけるシーケンス解析
各事例ではマルコフ過程がシンプルなモデルながらも、実用的な結果を提供していることが確認されます。
まとめ
マルコフ過程は、現在の状態に注目した予測手法として多くの分野で活用されます。
シンプルな数学的表現を利用して、現実の複雑なシステムの解析が可能な点が魅力です。
シミュレーションや統計学との連携により、応用範囲は今後も広がる可能性があります。
柔軟な考え方を取り入れることで、実世界の問題解決に役立つ手法として期待されます。
